Variational Information Maximizing Exploration
Minimal Inplementation of Variational Information Maximizing Exploration (VIME) to improve exploration in reinforcement learning environments with sparse rewards.

A Brief Intro to VIME
Why do we need VIME?
Variational Information Maximizing Exploration (VIME) aims to help an agent explore its environment better, especially when rewards are sparse or hard to find. In typical reinforcement learning, agents rely on rewards to learn what actions are valuable. However, in environments where rewards are rare or delayed, agents can struggle to learn effectively because they don’t receive enough feedback.
How does it work?
VIME solves this by giving the agent “intrinsic rewards,” which encourage it to seek out new or unknown areas in the environment, even without an immediate reward. These intrinsic rewards come from an information gain: every time the agent encounters a new or surprising situation, it updates its understanding of how the environment works, and VIME rewards it for that learning.
Mathematically, information gain for a state transition is defined as the change in the agent's posterior belief about the environment dynamics given new data. This is expressed as:
\[\text{Information Gain} = D_{\text{KL}}\left( p(\theta | \tau, a) \; || \; p(\theta | \tau) \right)\]where:
- $ D_{\text{KL}} $ is the Kullback-Leibler (KL) divergence,
- $ p(\theta | \tau) $ is the agent's prior belief about the environment dynamics (parameterized by $\theta$),
- $ p(\theta | \tau, a) $ is the posterior belief after observing a new action $ a $ and state transition $\tau$.
In simple terms, the KL divergence here measures how different the updated belief is from the prior belief. The more the belief changes, the more the agent has learned, which translates to higher information gain.
Step-by-Step Process
-
Dynamics Model: VIME uses a Bayesian model to represent the environment dynamics, which estimates the probability $ p(s' | s, a, \theta) $ of reaching a new state $ s' $ given the current state $ s $, action $ a $, and parameters $ \theta $.
-
Posterior Update: Every time the agent takes an action and observes a transition, it updates its model of the environment dynamics. This update changes the posterior distribution $ p(\theta | \tau, a) $, where $ \tau $ represents the transition data collected so far.
-
Intrinsic Reward Calculation: The intrinsic reward $ r_{\text{int}} $ is then calculated as the KL divergence between the updated posterior and the prior:
\[r_{\text{int}} = D_{\text{KL}}\left( p(\theta | \tau, a) \; || \; p(\theta | \tau) \right)\]This intrinsic reward encourages the agent to explore areas where its model has the most to learn.
-
Total Reward: The agent’s objective becomes maximizing the sum of both extrinsic rewards (from the environment) and intrinsic rewards:
\[R_{\text{total}} = R_{\text{extrinsic}} + \lambda \cdot R_{\text{int}}\]Here, $ \lambda $ is a scaling factor that balances exploration (intrinsic rewards) and exploitation (extrinsic rewards).
Why would VIME Work?
By maximizing information gain, VIME effectively motivates the agent to explore unfamiliar states that will help it learn more about the environment. This approach is particularly helpful in sparse reward settings because the agent doesn’t rely solely on external rewards but is guided by curiosity.
Training rewards visualization
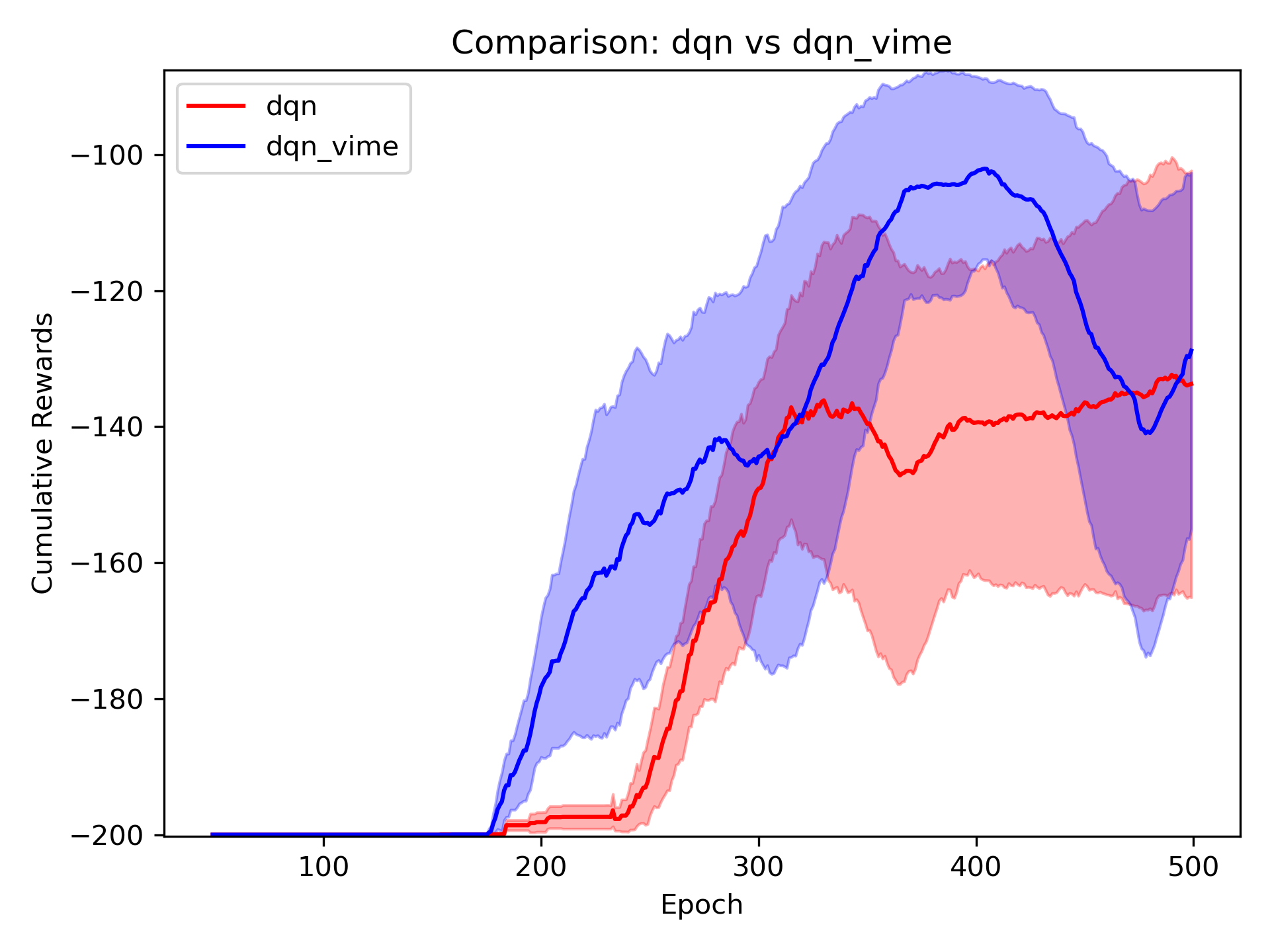
As we can see from the plot, DQN policy with VIME was able to reach higher peak rewards after training, and the reward was able to grow from ealier stage. These indicate the curiousity driven strategy of VIME enables better policy training.

