Uncertainty-Aware IRL from Suboptimal Demonstrations
Build rewards with a gaussian model to capture uncertainty for inverse reinforcement learning from Suboptimal Demonstrations
Motivation
Learning from Demonstration (LfD) allows agents to acquire behaviors from expert trajectories, but real-world demonstrations are often noisy, suboptimal, and inconsistent. Ranking-based LfD methods address this issue by learning from relative trajectory preferences, yet most ignore uncertainty in the learned reward, limiting robustness and downstream planning. We introduce Gaussian Ranking Inverse Reinforcement Learning (GR-IRL), a probabilistic framework that learns a distribution over rewards from ranked demonstrations by modeling both the expected reward and its uncertainty. This uncertainty-aware formulation enables more reliable reward inference, supports risk-sensitive planning, and improves policy learning in continuous-control tasks.
Method Overview
We learn a reward function from ranked, suboptimal demonstrations while explicitly modeling uncertainty. Our key idea is to represent the reward for each state–action pair as a Gaussian distribution, allowing the model to express confidence when ranking evidence is strong and caution when demonstrations are ambiguous.
The image below provides an intuition of the method:
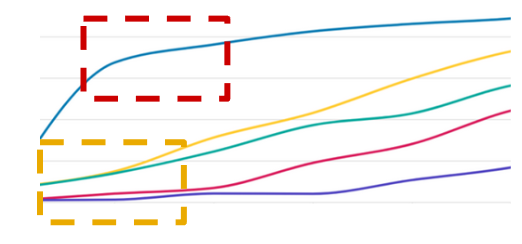
The plots consist of trajectories from demonstrators with varied experience levels. In the red region, the data will provide strong and consistent ranking signals, hence ideally it should be assigned with low variance. While in the yellow one, demonstrators with different rankings give similar demonstrations, making the ranking ambiguous, which should be associated with high variance.
Gaussian Reward Model
We model the reward as:
\[R(s,a) \sim \mathcal{N}\big(\mu_\theta(s,a), \sigma^2_\phi(s,a)\big),\]where neural networks predict both the mean reward \(\mu_\theta\) and the uncertainty \(\sigma^2_\phi\). High uncertainty naturally arises in regions where demonstrations overlap, preventing overconfident reward separation.
Ranking-Based Training
Given ranked trajectory pairs \((\tau_i \succ \tau_j)\), we optimize a likelihood that favors higher-ranked trajectories:
\[\mathcal{L}_{\text{rank}} = - \sum_{(i,j)} \log P(\tau_i \succ \tau_j).\]Trajectory preference is modeled using a softmax over cumulative rewards:
\[P(\tau_i) = \frac{ \exp\!\left( \sum_{(s,a)\in\tau_i} \hat{R}(s,a) \right) }{ \sum_k \exp\!\left( \sum_{(s,a)\in\tau_k} \hat{R}(s,a) \right) }.\]Uncertainty-Aware Likelihood
Exploiting the Gaussian reward form, we derive a closed-form expectation:
\[P(\tau_i) = \frac{ \exp\!\left( \sum \mu_\theta(s,a) + \tfrac{1}{2}\sum \sigma^2_\phi(s,a) \right) }{ \sum_k \exp\!\left( \sum \mu_\theta(s,a) + \tfrac{1}{2}\sum \sigma^2_\phi(s,a) \right) }.\]This formulation integrates uncertainty directly into ranking, enabling adaptive margins and more reliable reward inference. After training, the learned mean reward is used for downstream policy optimization with standard reinforcement learning algorithms.
Experiments
Setup
We evaluate GR-IRL on continuous-control MuJoCo benchmarks (Hopper-v3, Ant-v3, HalfCheetah-v3) and the Atari environment Breakout. Demonstrations are generated following the T-REX pipeline by checkpointing TRPO agents at different training stages to obtain trajectories of varying quality, which are then ranked to form preference data.
Evaluation Protocol
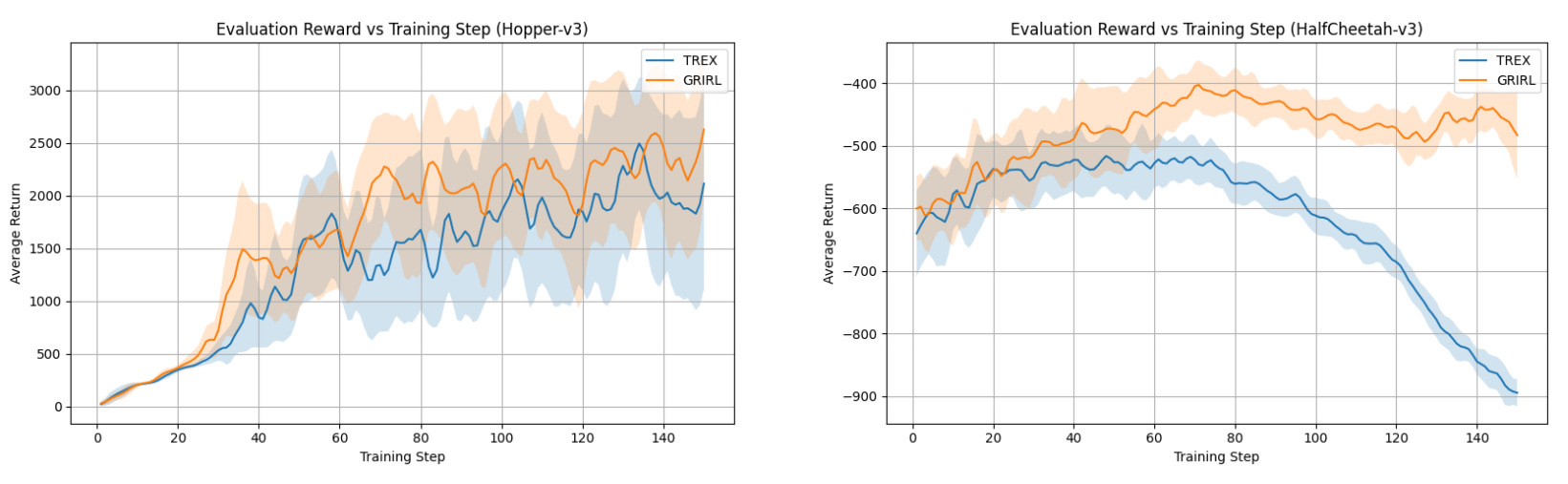
The reward model is trained on ranked trajectory pairs and outputs both a mean reward and uncertainty. To assess reward quality, we train downstream actor–critic policies using the mean predicted reward and compare their performance against policies trained with T-REX rewards.
Results
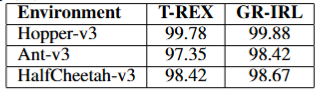
GR-IRL achieves slightly higher trajectory ranking accuracy than T-REX across all benchmarks, indicating comparable ability to capture coarse preferences. More importantly, policies trained with GR-IRL rewards consistently achieve higher returns than those trained with T-REX rewards, demonstrating that uncertainty-aware reward modeling leads to more effective policy learning.
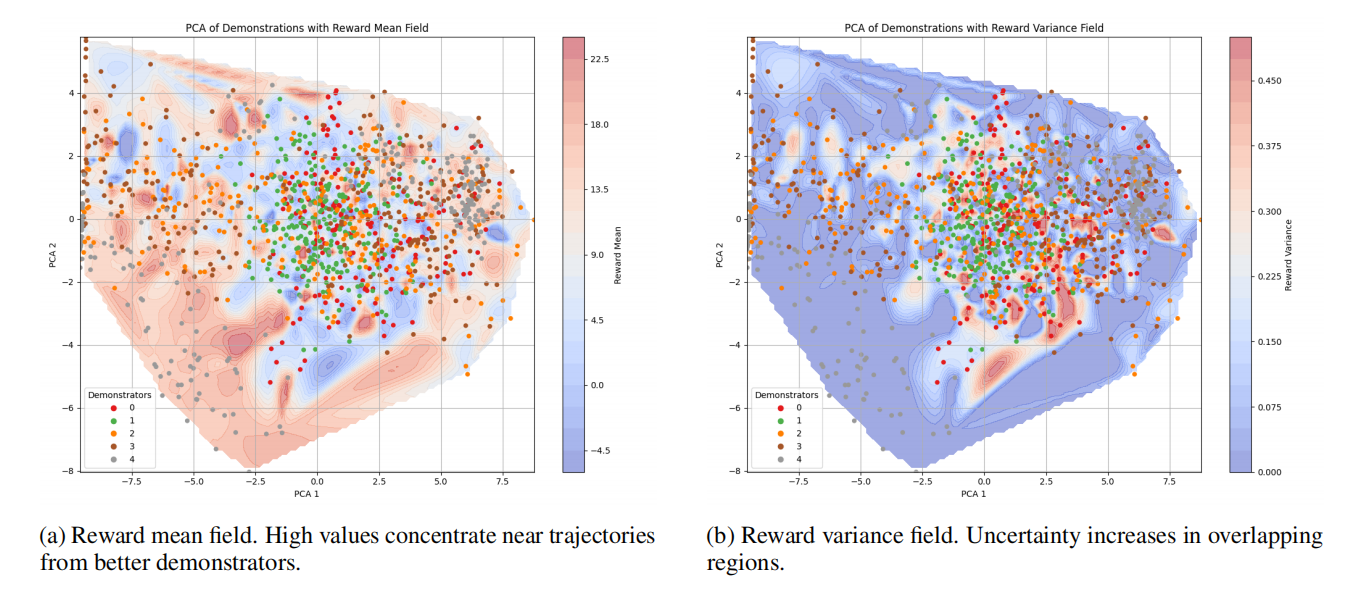
Reward Field Analysis
Visualizations in PCA space show that high-reward, low-variance regions align with expert demonstrations, while regions where trajectories overlap exhibit higher uncertainty. This behavior confirms that GR-IRL assigns confident rewards in unambiguous areas and remains cautious in ambiguous regions. In more complex tasks such as HalfCheetah-v3, greater trajectory overlap explains the increased difficulty of reward inference and the overall performance gap between environments.